Truss Analysis and Optimization
This project was for my Statics class. The assignment was to design, analyze, build, and test a simple planar truss from straws and foam gusset plates. The analysis was done in MATLAB using a program I wrote. I made sure to make the program very easy to use, so that new designs could be entered and analyzed very rapidly. I also wrote a optimization code that used iteration and a brute-force solver to optimize the truss for strength. I was the team leader for this project.



Introduction
The goal for the straw truss project was to design a simple, planar truss using MATLAB to perform a computational analysis, build the truss using the materials provided, and test the truss to determine the accuracy of our analysis. Every group in the class was given plastic drinking straws to use as members, foam core to use as gusset plates, and 'T' shaped hobby pins to secure the joints.
Design and Analysis
There are three basic aspects of truss design:
- Topology
- Geometry
- Member Size & Material
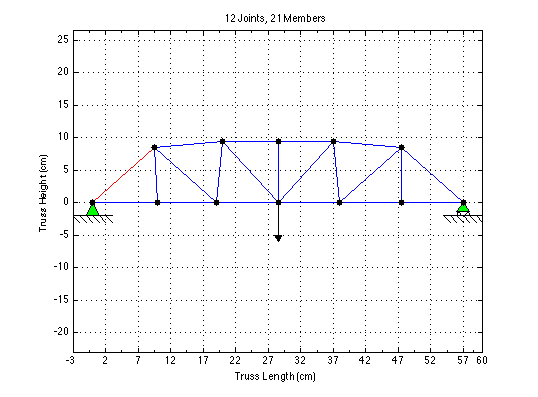
The topology of the truss is the number of nodes, the connections between them, and the supports of the truss. In our computational analysis, a connection matrix was defined that contained the information for the topology of the truss, and a support matrix contained information about where the truss was supported. The geometry of the truss concerns the location of the joints. The coordinates for each joint were stored in x and y position vectors for the computational analysis. Combined with the connection matrix, this allowed for the determination of the lengths and unit vectors for each member. Once the topology and geometry of the truss has been determined, an external load on the truss could be defined, and the forces in each member could be computed. Because the size and material of the members was already constrained (drinking straws were the required material), the buckling strength of each member, the maximum load the truss could sustain and the critical member(s) could be calculated using the member forces. The buckling strengths of the straws were based on data obtained from a lab testing the buckling strengths of different lengths of straws. In addition to this basic computational analysis, our group added an optimization feature to our program, which allowed a design to be refined. The optimization used a discrete combinatorial method and an exhaustive search to determine the best truss from a set of thousands of other trusses.